Bara

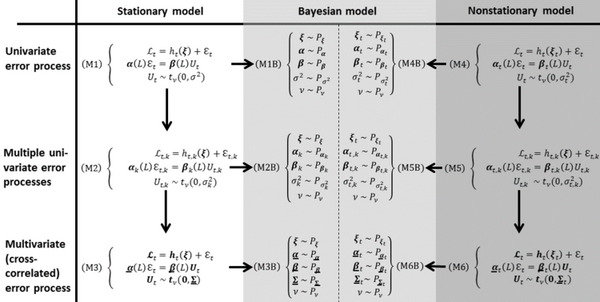
This research field aims at the development of a unified robust adjustment theory and of corresponding computationally efficient expectation maximization (EM) algorithms to handle outliers, data gaps, colored noise and cross-correlations within geodetic measurement series simultaneously. Various kinds of stationary and nonstationary Gauss-Markov models are investigated (see the figure below). To include given prior information for the unknown parameters, Bayesian models and inferential techniques are also devised. Applications include the geo-referencing of a static multi-sensor system and deformation monitoring of an arch bridge.

Modern geodetic sensors often produce multiple spatial time series which contain huge numbers of measurements, numerous outliers as well as data gaps, and random errors that are characterized by considerable auto- and cross-correlations (i.e., colored noise). In view of these adversities, which cannot be resolved by current geodetic data analysis tools in their entirety, we develop both classical and Bayesian statistics in connection with adjustment procedures that allow for a robust and efficient estimation of parametric models from such spatio-temporal measurement series.

To facilitate simultaneous robustness and statistical as well as computational efficiency, we employ on the one hand the principle of expectation maximization (EM). This enables an imputation of the data gaps and concurrently an adaptive estimation of the parameters of the functional model, of the coefficients of a vector autoregressive moving-average (VARMA) colored noise model, and of the shape parameters of the underlying error distribution. The latter is defined by a multivariate, scaled (Student's) t-distribution and involves a data-adaptable degree of freedom and scale factor. By estimating these quantities, the shape and in particular the tail characteristics of the probability density function is adapted to the actual error and outlier characteristics present in the data. We also allow for dynamic changes of the parameters of the functional and of the noise model.

Finally, we investigate Bayesian procedures based on Mean-Field Variational Bayes and Markov Chain Monte Carlo (MCMC) techniques, which allow for the incorporation of prior information regarding the parameters of the functional model, of the VARMA model and of the underlying t-distribution into the adaptive robust adjustment. Since the adjustment yields detailed probabilistic information regarding all of the unknown model parameters, we will for instance also be able to rigorously test hypotheses about the assumed error distribution, about suspected auto-/cross-correlation patterns, and about the time-variability of such patterns. We apply the static version of the general observation model and estimation procedure to adjustment problems based on geodetic data sets stemming from a geo-referencing of a  static multi-sensor-system, therein the referencing sensor can be 3D positioning sensors, like GNSS equipment or tacheometer. The dynamic version is applied to loading test data stemming from an arch bridge. Due to the anticipated high level of flexibility and efficiency of the methods, we expect that they may be applied also to other types of geodetic sensor data, as obtained e.g. in satellite geodesy.